2 Solving a Single Two-Dimensional Vector

In preparation to solve a single vector, trigonometry must be used. Based on our given values we can solve for a vector using cosine and sine. The given values are usually the angle of our vector, written as [latex]\theta[/latex], and your magnitude written as [latex]\vec{f}[/latex]. With both given values we can calculate the force in the 𝑥 and 𝑦 axis. These calculations are necessary for calculating the sum of more than one vector quantity.

However, before we fully indulge, I find importance in revisiting sine and cosine. As an early student I struggled with trigonometry as I did not understand what sine and cosine were. Were they numbers represented by words? Were they meaningless words derived from tables in pre-calculator mathematics? And why do we refer to sine as the 𝑦-axis, and cosine as the 𝑥-axis? 

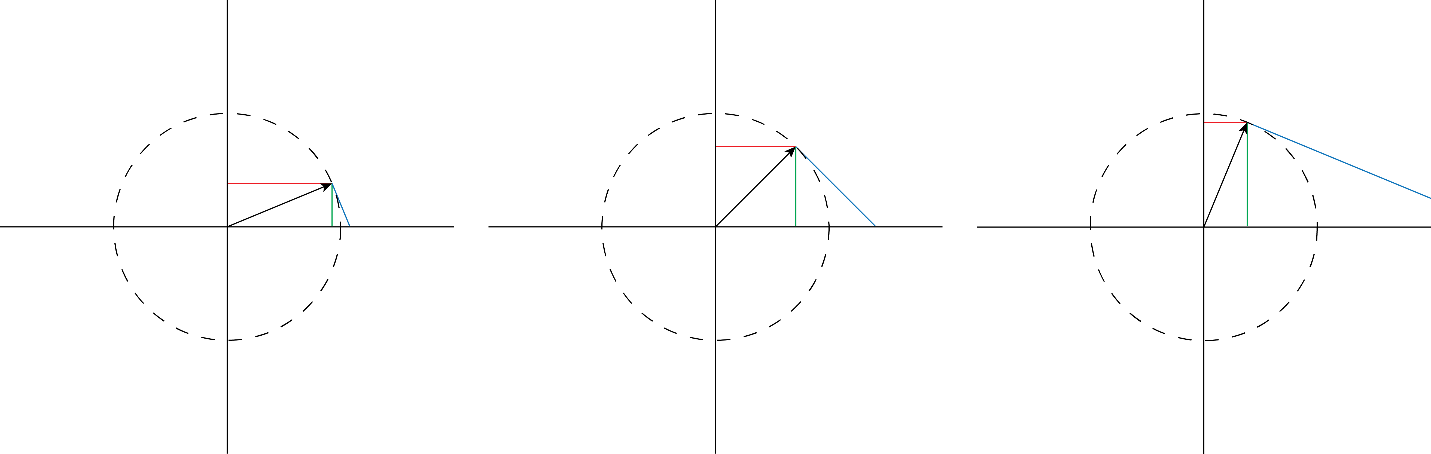
Please refer to Figure 2. It has a radius of one unit (inches well say). From the leftmost plane to rightmost, these three pictures describe SOH CAH TOA when the hypotenuse has an increasing angle. This is a triangle that has some special properties since it has a hypotenuse of one inch, commonly known as a unit circle. The angle inside the triangle that is in between the hypotenuse and the positive 𝑥-axis we call [latex]\theta[/latex].

The line that has been drawn from the point on the circumference to the 𝑥-axis we will label as [latex]opp[/latex], as in the opposite. You can then find the sine of the angle [latex]\theta[/latex]^[1], which is [latex]sin\theta=\frac{opp}{1}[/latex], rearranged, [latex]1\times sin\theta=opp[/latex]. This means that the line between the 𝑥-axis and the point on the circle is [latex]sin\theta[/latex]. This is why the 𝑦-axis is called the “sine” as that is what it represents on a triangle.

Much is interchangeable with cosine. Just shift that line from the 𝑥-axis now to the 𝑦-axis while maintaining the same position of the circle’s circumference we will call this length [latex]adj[/latex] for adjacent^[2]. Now we can find the “cosine” of [latex]\theta[/latex]^[3] which is [latex]cos\theta=\frac{adj}{1}[/latex], rearranged is [latex]1\times cos\theta=adj[/latex] which means that the length of the line between the origin and the 𝑦-intercept^[4] is [latex]cos\theta[/latex]. This is why the 𝑥-axis is called the “cosine” as it is what it represents on a triangle.

Since the base of the triangle is [latex]cos\theta[/latex] and the height is [latex]sin\theta[/latex] and the hypotenuse has a value of one inch, we can use Pythagorean theorem on this triangle to prove that [latex]{sin}^2\theta+{cos}^2\theta=1[/latex].

Now that we understand the basics of trigonometry, we can move into solving for our first vector. Observe figure 3 and ignore everything with a subscript of two until the next chapter, this information is not needed at this moment. The information we want to know is our [latex]\vec{f_1}[/latex], [latex]f_{1x}[/latex], [latex]f_{1y}[/latex], and our [latex]\theta_{1xy}[/latex]. Typically, your givens will be your [latex]\theta_{1xy}[/latex] and your [latex]\vec{f_1}[/latex]. Utilizing trigonometry, we can solve for the triangle to obtain our [latex]f_{1x}[/latex] and our [latex]f_{1y}[/latex] values. This is essential for determining the amount of force in a certain direction since your force in your 𝑥-axis is completely independent of the force in your 𝑦-axis. This is the system that will be used alongside my equations for the entirety of two-dimensional linear vector addition.

A way to think about this phenomenon is swimming in a river with a fast current. If you are in the middle of the river and you want to swim to shore as quickly as possible, how should you swim relative to the flow of the river? You should swim perpendicularly to the current. Any force you put into swimming with or against the current will be counteracted by the water. The river has no force perpendicular to its flow therefore if you swim perpendicular to the current you will be moving at a velocity as if you were in a stagnant pool^[5].

When solving vector addition, we are looking for the resultant. Our resultant is the sum of our forces in the 𝑦 and 𝑥 axis alongside the sum of angles. In this scenario, we are only given one vector with our magnitude and angle as our given values. Our resultant, or the sum of all directional forces, in this case is simply our magnitude, and our direction is our final direction.

Let us now solve for a single vector. Our givens are a magnitude of 20 kilos represented as [latex]\vec{f}[/latex], and a direction of [latex]{40}^\circ[/latex] represented by [latex]\theta_{xy}[/latex]. We know that this vector will be in the first quadrant, where both 𝑦 and 𝑥 are positive, that said our [latex]f_x[/latex] and [latex]f_y[/latex] will both be positive. Utilizing the equations, we know we can begin by solving for our [latex]f_x[/latex];

[latex]\left(cos{40}^\circ=\frac{f_x}{20kg}\right)=15.32kg[/latex]

Now that we know what our 𝑥 value is, we can either use Pythagorean theorem to solve for the final side, or we can use the previously stated sine equation. Checking your work can save you loads of trouble down the line. I find safety in solving the final side by using the theorem and then checking with sine.  This value is positive, which verifies our position along the 𝑥 axis. When solving for our 𝑦 value, no matter the way you chose, the answer is 12.85kg rounded to two decimal places. This value is also positive, confirming our hypotheses.

You can also reverse the process if you are given your 𝑥 and 𝑦 values and are searching for your resultant and your angle. You can use Pythagorean theorem to solve for your hypotenuse, and then you can solve for the angle with the same equation stated early simply rearranged.