8 Solving a Single Three-Dimensional Vector

Solving for a three-dimensional vector is straightforward; you need to solve for two triangles. These Triangles are both right triangles so the most basic trigonometry ratios can be utilized. The majority of calculations will be the same as for the previous part of this paper, however a few additions have been made, most notably, a third axis. This axis is labeled as [latex]z[/latex] and nearly everything^[1] that involves said axis is new to this chapter and will build on the knowledge previously gained from earlier chapters. These new additions include, [latex]f_{iz}[/latex] and [latex]\theta_{ixyz}[/latex]. These values represent similar things to those previously stated, the major difference being that they are in a new plane and are independent of the values in the [latex]x[/latex] and [latex]y[/latex] axis. Another major change is that what we have previously known as the vector in two dimensions, is now referred to as [latex]f_{ixy}[/latex]. Not unlike the last chapter, all numerical values within the subscript are to be ignored for this chapter as it too will only be of use to us later on. We do not need these values for the sole reason that we are only solving for one vector.

Momentarily I will present my system for my third, fourth and fifth equations. Before I do however, I would like to explain exactly what you are looking at. Exhibit the following hyperplane shown in figure 6. The solid lines without arrow tips are the axis of the plane, the solid line with the arrow is the vector, the broken lines are the coordinates that we are solving for, and the line broken in the middle is essentially the shadow cast by the vector during a noon sun. The halved line is the hypotenuse of the [latex]xy[/latex] plane and will be used to solve for a second hypotenuse in the [latex]xyz[/latex] plane. This line is literally the vector from part one and we will be solving for it the same way.

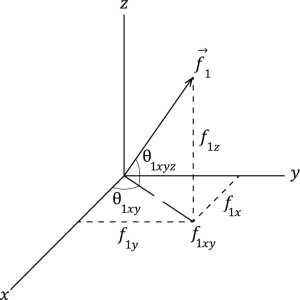
This is the system we will be using to solve for our three-dimensional vectors. Keep in mind that all the dotted lines do is give you a visual representation of the [latex]x,\ y[/latex] and [latex]z[/latex] coordinates of the vector. I have arranged said lines in a way that corresponds with the order that we solve the vector for, we need the [latex]x[/latex] and [latex]y[/latex] coordinates for the halved line, but not the vector line as we use the halved line to solve for it, meaning that we use the [latex]z[/latex] coordinate and the half line to solve for the vector.

The time has now come that we solve for a single three-dimensional vector. This solution is very straightforward and only requires SOH CAH TOA to be completed. Our givens for this problem will be our vector, written as [latex]\vec{f_1}[/latex], and our two angles [latex]\theta_{1xyz}[/latex] and [latex]\theta_{1xy}[/latex]. In this problem we are looking for our [latex]x,\ y[/latex] and [latex]z[/latex] lengths, or the coordinates of the vector tip. I have written the values as such that you can find them on the hyperplane, but from here on out I will be removing the numbers in the subscript to simplify the process, as we only have one vector. The process we will take is as follows: we will use cosine to solve for any value containing [latex]x[/latex] in the subscript, and sine for the remaining [latex]f_x[/latex] value.

Our values are as follows: a magnitude of [latex]2[/latex] units, a direction in the [latex]z[/latex] axis of [latex]{30}^\circ[/latex] and a direction in the [latex]xy[/latex] axis of [latex]{55}^\circ[/latex]. Firstly, we will solve for the [latex]f_{xy}[/latex] using cosine,

[latex]\left(cos{{30}^\circ}_{xyz}=\frac{f_{xy}}{2}\right)=\sqrt3[/latex]

We can now plug this value into cosine once more to solve for our axis,

[latex]\left(cos{55}^\circ=\frac{f_x}{\sqrt3}\right)=0.993[/latex]

From here we can go one of two ways, we can solve the remaining side by way of sine, or Pythagorean theorem. Personally, I prefer to solve with sine and then check with Pythagorean theorem,

[latex]\left(sin{55}^\circ=\frac{f_y}{\sqrt3}\right)=1.41[/latex]

Now we have only one axis to solve for, our [latex]z[/latex] axis,

[latex]\left({sin30}^\circ=\frac{f_z}{2}\right)=1[/latex]

Therefore, our coordinates for a vector with a magnitude of [latex]2[/latex] units and a direction in the [latex]z[/latex] axis of [latex]{30}^\circ[/latex] and a direction in the [latex]xy[/latex] axis of [latex]{55}^\circ[/latex] is 0.993, 1.41, 1 (stated in order of [latex]xyz[/latex]).

Once more, you can reverse the process we took to solve for the magnitude of the vector in a scenario where your givens are your coordinates.